When it comes to understanding data, mean, median, and mode are like the holy trinity of statistics. They’re the building blocks that help us make sense of numbers, trends, and patterns. Whether you’re a student trying to ace your math exam, a data analyst crunching numbers for a project, or just someone curious about how numbers work, knowing the connections between mean, median, and mode is essential. So, buckle up, because we’re diving deep into the world of averages and central tendencies!
Let’s face it, math can sometimes feel like a foreign language. But when you break it down, concepts like mean, median, and mode become way more approachable. These three terms are all about finding the center of a dataset. They each tell us something different, but together, they create a complete picture of what the data is really saying. Think of them as friends who bring different perspectives to the table.
In this article, we’ll explore how mean, median, and mode connect, why they matter, and how to use them in real-life situations. By the end, you’ll have a solid grasp of these statistical tools and be ready to tackle any dataset that comes your way. Trust me, it’s gonna be a wild ride!
Read also:Scrambled Eggs Pudding The Creamy Cheesy Delight Thats Taking Breakfast To The Next Level
Here’s a quick guide to help you navigate through this article:
- What is Mean?
- What is Median?
- What is Mode?
- Connections Between Mean, Median, and Mode
- Practical Applications
- How to Calculate Mean, Median, and Mode
- Real-World Examples
- Common Mistakes to Avoid
- Why Mean, Median, and Mode Matter
- Conclusion
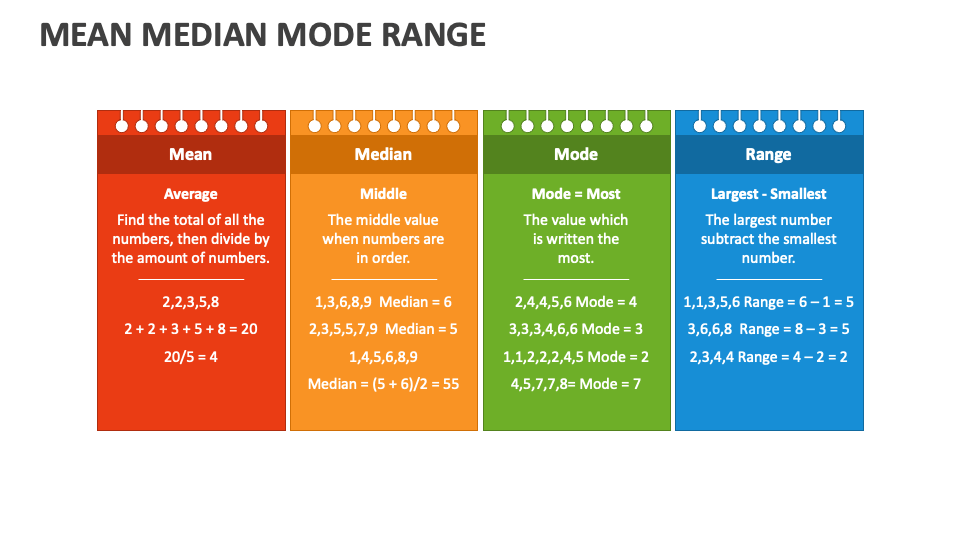
What is Mean?
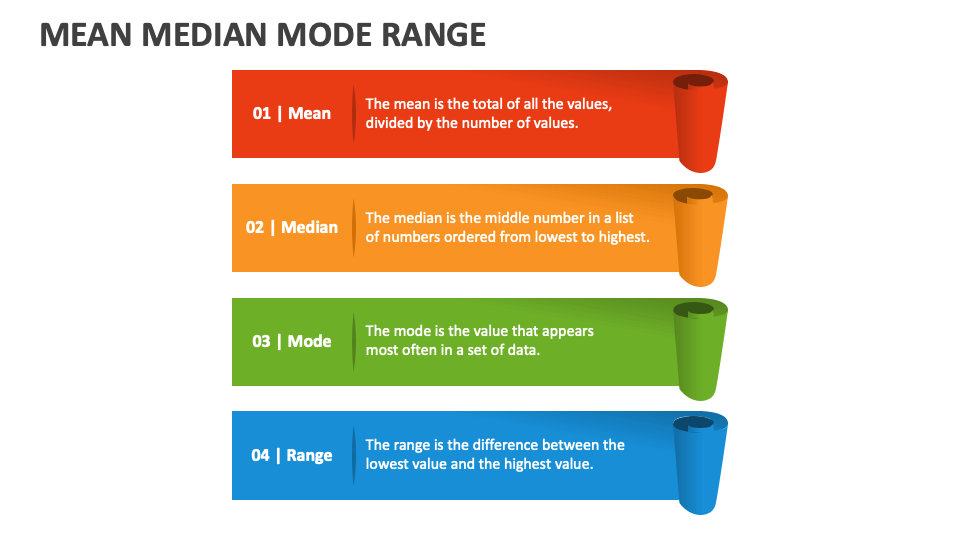
The mean, or average, is like the star of the show in the world of statistics. It’s calculated by adding up all the numbers in a dataset and then dividing by the total count. Simple, right? But don’t let its simplicity fool you. The mean is incredibly powerful and widely used in everything from academic research to business analytics.
Here’s a quick example to illustrate how it works. Let’s say you have a dataset with the following numbers: 5, 10, 15, 20, and 25. To find the mean, you add them all up (5 + 10 + 15 + 20 + 25 = 75) and then divide by the total count (5). So, the mean is 15. Easy peasy!
But here’s the thing – the mean isn’t always perfect. It can be skewed by outliers, those pesky numbers that are way higher or lower than the rest. For example, if you add a 100 to the dataset above, the mean jumps up to 25. That’s where the median comes in, but we’ll get to that later.
Why Mean is Important
The mean gives us a single value that represents the entire dataset. It’s great for summarizing large amounts of data and spotting trends. For instance, if you’re analyzing the average income of a city, the mean can give you a quick snapshot of the financial health of its residents.
However, always remember that the mean doesn’t tell the whole story. It’s just one piece of the puzzle. To get the full picture, you need to consider the median and mode as well.
Read also:Mastering The Art Of Masc Eyeliner Your Ultimate Guide
What is Median?
Alright, let’s talk about the median. Think of it as the middle child of the statistical family. The median is the number that sits right in the middle when you arrange all the numbers in a dataset in ascending order. No fancy calculations here – just good old sorting.
Let’s revisit our previous dataset: 5, 10, 15, 20, 25. When arranged in order, the middle number is 15. That’s the median. But what if you have an even number of values? In that case, you take the average of the two middle numbers. For example, if the dataset is 5, 10, 15, 20, the median would be (10 + 15) / 2 = 12.5. Pretty straightforward, huh?
The median is especially useful when dealing with datasets that have outliers. Unlike the mean, it isn’t affected by extreme values. This makes it a more reliable measure of central tendency in certain situations.
When to Use Median
Imagine you’re looking at house prices in a neighborhood. If there’s one mansion that costs millions while the rest are modest homes, the mean price would be misleadingly high. The median, on the other hand, would give you a more accurate representation of what most people in the area can afford. That’s why real estate agents love it!
What is Mode?
Now, let’s meet the quirky sibling of the trio – the mode. The mode is the number that appears most frequently in a dataset. It’s like the popular kid in school, always showing up and getting noticed. If no number repeats, then there’s no mode. And if two or more numbers have the same highest frequency, you have multiple modes.
Let’s say you have the following dataset: 3, 5, 5, 7, 9. The number 5 appears twice, while all the others appear only once. So, the mode is 5. Simple enough, right?
The mode is particularly useful when dealing with categorical data, like favorite colors or types of pets. It helps identify the most common category, making it a valuable tool in market research and surveys.
Limitations of Mode
While the mode is great for identifying trends in categorical data, it’s not always the best choice for numerical data. For example, in a dataset where all numbers are unique, the mode doesn’t exist. And in datasets with multiple modes, it can be tricky to interpret the results. But hey, every tool has its limitations, right?
Connections Between Mean, Median, and Mode
So, we’ve talked about mean, median, and mode individually, but how do they relate to each other? The connections between them can tell us a lot about the shape and distribution of a dataset.
In a perfectly symmetrical distribution, like a bell curve, the mean, median, and mode are all the same. But in skewed distributions, they start to diverge. For example, in a positively skewed distribution (where the tail is on the right), the mean is usually greater than the median, and the mode is the smallest. In a negatively skewed distribution (where the tail is on the left), the opposite is true.
Understanding these relationships helps us interpret data more accurately. It’s like having three different lenses to view the same picture. Each one highlights a different aspect, and together, they create a richer understanding.
Key Takeaways
- In symmetric distributions, mean = median = mode.
- In positively skewed distributions, mean > median > mode.
- In negatively skewed distributions, mean
Practical Applications
Now that we’ve covered the theory, let’s talk about how mean, median, and mode are used in real life. These statistical tools aren’t just for math geeks; they’re applied in a wide range of fields, from healthcare to finance to sports analytics.
In healthcare, for example, the mean is often used to calculate average patient outcomes, while the median is used to determine the typical recovery time. In finance, the mode can help identify the most common stock price or interest rate. And in sports, the median is a great way to compare athletes’ performances without being skewed by outliers.
The possibilities are endless, and the insights gained from these tools can drive decision-making and improve outcomes across industries.
Case Study: Analyzing Test Scores
Let’s say you’re a teacher analyzing your students’ test scores. The mean gives you the overall performance, the median tells you the middle score, and the mode shows you the most common score. Together, they help you identify strengths, weaknesses, and areas for improvement.
How to Calculate Mean, Median, and Mode
Calculating mean, median, and mode might sound intimidating, but it’s actually pretty simple. Here’s a step-by-step guide:
Calculating Mean
- Add up all the numbers in the dataset.
- Divide the total by the number of values.
Calculating Median
- Arrange the numbers in ascending order.
- Find the middle number. If there’s an even number of values, take the average of the two middle numbers.
Calculating Mode
- Count how many times each number appears in the dataset.
- The number with the highest frequency is the mode. If no number repeats, there’s no mode.
Real-World Examples
To make things more relatable, let’s look at some real-world examples of mean, median, and mode in action.
Example 1: Income Analysis
In a city where most people earn around $50,000 per year, but a few billionaires skew the average income to $1 million, the median income provides a more accurate representation of the typical resident’s financial situation. In this case, the median is much lower than the mean.
Example 2: Customer Preferences
A coffee shop owner wants to know which drink is the most popular. By calculating the mode of customer orders, they discover that latte is the clear winner. This insight helps them optimize their menu and marketing strategy.
Common Mistakes to Avoid
Even the best statisticians make mistakes sometimes. Here are a few common pitfalls to watch out for:
- Using the mean when the dataset has outliers.
- Forgetting to arrange numbers in order before finding the median.
- Assuming that every dataset has a mode.
By being aware of these mistakes, you can ensure your analysis is accurate and reliable.
Why Mean, Median, and Mode Matter
At the end of the day, mean, median, and mode matter because they help us make sense of the world around us. Whether you’re analyzing data for work, school, or personal interest, these tools provide valuable insights that can inform decisions and drive success.
They’re not just abstract concepts; they’re practical tools that have real-world applications. So, take the time to understand them, and you’ll be amazed at how much they can teach you.
Conclusion
In conclusion, mean, median, and mode are the backbone of statistical analysis. Each one offers a unique perspective on data, and together, they create a comprehensive view of what the numbers are really saying. By understanding their connections and applications, you can unlock the power of data and use it to your advantage.
So, the next time you’re faced with a dataset, don’t panic. Just remember the trio of mean, median, and mode, and you’ll be good to go. And don’t forget to share this article with your friends and colleagues – knowledge is power, and the more people who understand these concepts, the better!